Кривые доходности для свопов

Кривая доходности свопа

Кривая доходности свопа – это графическое представление зависимости фиксированных ставок по процентным свопам от их срока.

Для целей оценки процентный своп можно представить, как серию купонных платежей по воображаемой синтетической облигации с фиксированной ставкой на стороне фиксированного процента против серии процентных платежей по воображаемой синтетической облигации с плавающей ставкой (floating rate note – FRN) на стороне плавающего процента.

Кривую доходности свопа можно рассматривать как кривую доходности синтетических облигаций с фиксированной ставкой.

Пример: сторона фиксированного процента – простая облигация, сторона плавающего процента – облигация с плавающей ставкой (FRN).

Предположим, что между корпорацией XYZ и банком ABC заключено соглашение о простом свопе с условной основной суммой $100 млн. сроком на 3 года. На стороне фиксированного процента выплаты производятся по ставке 9,30% в годовом исчислении, на стороне плавающего процента – по 12-месячной ставке LIBOR.

Потоки денежных средств в течение трёхлетнего периода представлены графически на схеме внизу.

Рис.1 Схема потока денег.

Таким образом, простой процентный своп можно оценить следующим образом: Текущая стоимость условной простой облигации – Текущая стоимость условного инструмента с плавающей ставкой

XYZ и АСВ заключили соглашение о свопе на следующих условиях. На дату «спот» ставка LIBOR зафиксирована на уровне 7,50% для первого платежа. В начальный момент своп не имеет стоимости. На дату первого платежа ставка трёхлетнего свопа котируется на уровне 9,00% (сторона фиксированного процента), а 12-месячная LIBOR зафиксирована на уровне 7,79%. Чему равна стоимость свопа теперь? Является ли своп для получателя фиксированной стороны активом, или же это пассив?

Как определить текущую стоимость свопа, срок которого наступает в будущем? Текущую стоимость фиксированной стороны можно рассчитать по формуле определения стоимости простой облигации. Для облигации с годовым купоном это формула 1:

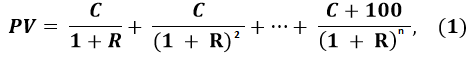
где:

• С – купонная ставка
• R – учётная ставка или ставка свопа в виде десятичной дроби
• n – число лет до погашения

В данном случае:

• С = 9,30%
• R = 0,090%
• n = 3

следовательно:

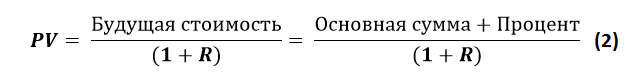
Текущую стоимость для стороны плавающего процента можно рассчитать, используя зависимость между текущей и будущей стоимостью инструмента, по формуле 2:

где:

• R – учётная ставка или LIBOR в виде десятичной дроби

В данном примере основная сумма составляет $100 млн., процент – 7,50%, a R – 0,0779. Поскольку годовая база плавающей ставки – 360 дней (А/360), стоимость следует привести к годовой базе 365 дней:

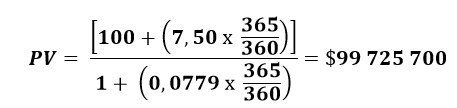
Таким образом, нетто-стоимость свопа составляет $1,03 млн. в пользу стороны фиксированного процента. Это объясняется тем, что ставка свопа, прокотированная банком в конце первого платежного периода, ниже купонной ставки в 9,30%. Снижение стоимости на стороне плавающего процента связано с ростом ставки LIBOR.

Подход к оценке свопа на основе разницы между стоимостью простой облигации и стоимостью инструмента с плавающей ставкой позволяет маркет-мейкерам хеджировать или «складировать» своп-позицию с помощью временной покупки или продажи базового актива – облигации.

Плательщик фиксированной ставки покупает базовый инструмент, который затем может продать с целью зачёта позиции, если ставки свопа падают.

Получатель фиксированной ставки продает базовый инструмент, чтобы компенсировать убытки в случае роста ставок свопа.

Расчёты здесь сложные и требуют времени. На практике трейдеры часто пользуются графиками для оценки свопа относительно инструментов с таким сроком, выбранных в качестве ориентира. Подобным графиком является кривая спот-ставок (spot curve), или кривая доходности нулевого купона (zero coupon yield curve).

Оценка на основе кривой спот-ставок

Кривая доходности при погашении (YTM) для облигаций – это просто график зависимости значений YTM от срока. К сожалению, такой подход чрезмерно упрощает ситуацию, поэтому правильней будет использовать график зависимости спот-ставок от срока. Спот-ставка – это измеритель YTM финансового инструмента в любой момент времени, который учитывает различные рыночные факторы. График «спот-ставка – срок» называют кривой спот-ставок или кривой доходности нулевого купона, поскольку спот-ставка по инструменту эквивалентна доходности инструмента без купонных выплат, то есть инструмента с нулевым купоном. Это означает, что спот-ставки серии инструментов с нулевыми купонами и различными сроками можно сравнить напрямую.

Кривые отражают зависимость между доходностью инструмента и сроком его действия, измеряемым обычно в годах. В зависимости от формы кривая может быть:

1. Положительной.
2. Отрицательной (обратной).

Положительная кривая доходности

В этом случае краткосрочные процентные ставки ниже, чем долгосрочные. Именно такая ситуация наблюдается чаще всего: чем больше инвестиционный период, тем выше выплачиваемый доход. В ожидании повышения процентной ставки инвесторы начинают вкладывать активы в долгосрочные инструменты, что вызывает снижение краткосрочных ставок и рост долгосрочных.

Отрицательная или обратная кривая доходности

Когда краткосрочные ставки падают, инвесторы перемещают свои вложения в долгосрочные финансовые инструменты, чтобы получить более высокий доход. Рост предложения долгосрочных финансовых ресурсов приводят к снижению долгосрочных ставок.

Формы «теоретических» кривых доходности показаны ниже, однако на практике они не идеальны!

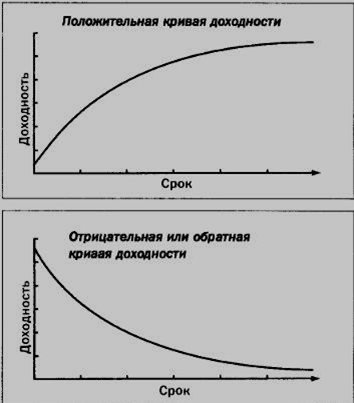
Рис. 2 Кривые доходности.

Кривые доходности позволяют идентифицировать различия финансовых инструментов с сходными кредитными характеристиками, например, процентного свопа и казначейской облигации с одинаковыми сроками.

Приведённая далее таблица помогает оценить стоимость инструмента на основе кривой спот-ставок.

Таблица 1. Оценка стоимости на основе кривой спот-ставок.

Как с помощью кривой спот-ставок оценить своп? Для большей точности представим процентный своп в виде последовательных потоков наличности по фиксированной ставке, с одной стороны, в сочетании с последовательными условными потоками наличности по плавающей ставке, с другой стороны, которые можно рассматривать как стрип FRA или фьючерсных контрактов.

Значения ставок, определённые по кривой, позволяют заранее рассчитать размер нетто-платежа для каждой будущей платежной даты.

Ставка свопа фактически равна средней ставке стрипа FRA или фьючерсных контрактов. Расчёты здесь сложные, поэтому отметим только, что в случае использования в предыдущем примере этого более точного метода нетто-стоимость свопа составила бы $1,043 млн. в пользу стороны фиксированного процента.