Содержание
Давайте разберёмся более основательно в следующих понятиях:
- Различия между свопами;
- Спред свопа;
- Процедуры оценки свопов.
Различия между свопами
Существует четыре основных различия между свопами.
Условия котирования
На рынках, в частности американских, существуют различные подходы к определению размера процентных платежей по фиксированной и плавающей ставке, кроме того, различной может быть и периодичность выплат. В свопах применяются комбинации следующих условий.
Таблица 1. Условия по свопам.
| Условия | Фиксированная ставка | Плавающая ставка |
| Котировка ставки |
|
|
| Периодичность платежей |
|
|
| База |
|
|
Базовые финансовые инструменты
Финансовые инструменты, используемые для исчисления своп-ставок по различным валютам, могут быть разными. Например, свопы на американские доллары обычно котируются как спред относительно соответствующего казначейского инструмента с полугодовыми купонами. Свопы на швейцарские франки котируются относительно годовых евробондов.
Таблица 2. Финансовые инструменты, используемые для основных валют, а также годовые базы для исчисления процентных платежей.
| Валюта | Котируется как… | Купон | База для расчёта (количество дней) |
| USD | Спред относительно казначейской облигации | полугодовой | Фактическое/Фактическое |
| CHF | Фиксированный евробонд | годовой | 30/360 |
| GBP | Спред относительно золотообрезной ценной бумаги | полугодовой | Фактическое/365 |
| JPY | Фиксированная правительственная облигация | полугодовой | Фактическое/365 |
Периодичность процентных платежей
Для корректного сравнения своп-ставок необходимо перевести годовые платежи в полугодовые, или наоборот.
Таблица 3. Формулы преобразования доходности или своп-ставки.
| Из → | В → | Формула |
| полугодовых | годовые | 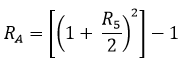 |
| годовых | полугодовые | 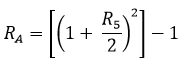
|
Годовая база
При сопоставлении свопов и их оценке в некоторых случаях приходится пересчитывать своп-ставки для приведения их к одной годовой базе.
Таблица 4. Способы приведения годовых баз.
| Из → | В → | Способ пересчёта |
| 30/360 или фактическое/365 | Фактическое/360 | Доходность х 360/365 |
| Фактическое/360 | 30/360 или фактическое/365 | Доходность х 365/360 |
| Фактическое/365 | 30/360 | Пересчёта не требуется |
| 30/360 | Фактическое/365 | Пересчёта не требуется |
Спред свопа
Характер движения процентных ставок влияет на спред свопов относительно кривых доходности правительственных финансовых инструментов-ориентиров:
- В ожидании падения процентных ставок у многих эмитентов инструментов с фиксированной ставкой появляется желание перейти на выплаты по плавающей ставке в обмен на получение платежей по фиксированной, поэтому спреды сужаются;
- В ожидании роста процентных ставок многие заёмщики стремятся перейти на выплаты по фиксированной ставке, однако мало кто желает получать платежи по фиксированной ставке, поэтому спреды расширяются;
- Другим фактором, влияющим на спред свопов, является кредитный риск. В свопе участник рынка и маркет-мейкер несут взаимный риск. Если одна из сторон оказывается неспособной выполнить платёжные обязательства, то другая сторона подвергнется нежелательному процентному риску.
В валютно-процентных свопах платежи осуществляются как по фиксированной, так и по плавающей ставке, поэтому определение риска убытков следует проводить с учётом волатильности базы будущей плавающей ставки, например, LIBOR.
Расчёт свопов
Своп-ставки являются индикатором текущего значения форвардных процентных ставок. Фиксированная своп-ставка – это средняя величина плавающей ставки за весь период действия контракта, устанавливаемая соглашениями о будущей процентной ставке.
Пример 1
5-летний валютно-процентный своп с фиксированной/плавающей ставкой, в котором Компания и Банк обменивают $100 млн. на 170 млн. франков по спот-курсу USD/CHF = 1,7000. Каждые 6 месяцев Компания выплачивает Банку фиксированную ставку 6% в марках, а Банк выплачивает Компании плавающую ставку LIBOR в долларах.
Спот-курс для свопа установлен на 1 июня, поэтому первый платёж должен быть осуществлен 1 декабря. Размер причитающегося на 1 декабря процентного платежа известен уже 1 июня. Потому что ставка LIBOR фиксируется 1 июня для плавающего платежа, который должен быть сотворён через 6 месяцев. Ставка LIBOR для следующего платежа фиксируется 1 декабря, а затем через каждые полгода на протяжении всех пяти лет вплоть до последнего платежа.
В целях оценки этот своп с фиксированной/ плавающей ставкой можно рассматривать как серию купонных платежей по воображаемой простой облигации на стороне фиксированного процента против серии платежей по воображаемой или синтетической облигации с плавающей ставкой (FRN) на стороне плавающего процента.
Текущую стоимость фиксированной стороны можно рассчитать на основе формулы определения стоимости простой облигации. Для облигации с годовым купоном это формула 1:
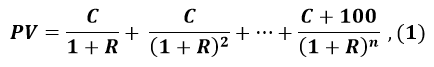
где:
- С – купонная ставка
- R – учётная ставка или своп-ставка в виде десятичной дроби
- n – количество лет до погашения
Текущую стоимость для стороны плавающего процента можно рассчитать, используя зависимость между текущей и будущей стоимостями инструмента, по формуле 2:
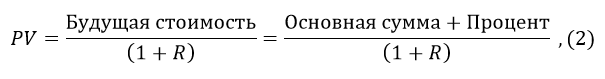
Оценка на основе кривой спот-ставок
Кривая доходности при погашении (YTM) для облигаций – это просто график зависимости значений YTM от срока. Такой подход упрощает ситуацию, поэтому правильней использовать график зависимости спот-ставок от срока.
Спот-ставка – это измеритель YTM финансового инструмента в любой момент времени, который учитывает различные рыночные факторы.
График «спот-ставка – срок» называют кривой спот-ставок или кривой доходности нулевого купона, поскольку спот-ставка по инструменту эквивалентна доходности инструмента без купонных выплат, то есть инструмента с нулевым купоном. Это означает, что спот-ставки серии инструментов с нулевыми купонами и различными сроками можно сравнить напрямую.
Нулевой купон можно рассматривать как кривую дисконтирования для больших сроков.
Кривые отражают зависимость между доходностью инструмента и сроком его действия, измеряемым в годах. В зависимости от формы кривая может быть:
- положительной
- отрицательной или обратной
Положительная кривая доходности
В этом случае краткосрочные процентные ставки ниже, чем долгосрочные. Именно такая ситуация наблюдается чаще всего, – чем больше инвестиционный период, тем выше выплачиваемый доход.
Отрицательная или обратная кривая доходности
Когда краткосрочные ставки падают, инвесторы перемещают свои вложения в долгосрочные финансовые инструменты, чтобы получить более высокий доход. Рост предложения долгосрочных финансовых ресурсов вызывает снижение долгосрочных ставок.
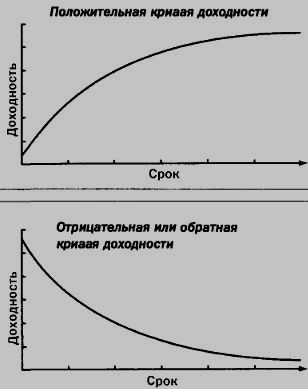
Рис. 1. Формы «теоретических» кривых доходности.
Кривые доходности позволяют идентифицировать различия финансовых инструментов с сходными кредитными характеристиками, например, процентного свопа и казначейской облигации с одинаковыми сроками.
Трейдеры могут сравнить спреды разных инструментов по отношению к кривой спот-ставок и определить дешевые они или дорогие. Из двух инструментов с одинаковыми кредитными характеристиками и сроками более дешевым будет тот, у которого спред шире.
Пример 2
Банк определяет ставки по валютно-процентному свопу с сроком погашения 1 год, в котором он платит фиксированную ставку, а получает платежи по плавающей 6-месячной ставке LIBOR. Плавающие ставки уже известны из кривой LIBOR, спрашивается, какую ставку следует установить на фиксированной стороне свопа?
Прибыльность свопа – нулевая, если чистая текущая стоимость двух платежей по 6-месячной плавающей ставке равна процентным платежам по фиксированной ставке. Ставка LIBOR на начало действия свопа равна 9%.
Вторая 6-месячная ставка LIBOR определяется по кривой ставок LIBOR:
- 6 месяцев – 9,00%
- 12 месяцев – 9,50%
- 18 месяцев – 10,00%
Доход на один вложенный доллар по ставке LIBOR, равной 9,00%, за 6 месяцев составит $0,045, поэтому через 6 месяцев стоимость инвестированного доллара будет равна $1,045. 12-месячная ставка LIBOR в примере – 9,50%. Какой должна быть вторая 6-месячная ставка LIBOR, чтобы превратить вложенные $1,045 в $1,095?
Для расчёта применяется формула 2:

Таким образом, ставка для 6-месячного периода составляет 2 х 0,04785 = 9,57%. Это величина ожидаемой 6-месячной ставки через 6 месяцев, полученная на основе кривой доходности. Иными словами, $1,045, инвестированные на полгода под 9,57%, дадут $1,095.
Итак, плавающие ставки для двух платежей равны соответственно 9,00% и 9,57%. Теперь на основе этих ставок можно определить размер фиксированной ставки, для чего нужно уравнять платежи по обеим сторонам, то есть привести их к уровню безубыточности.
Процентные платежи дисконтируются до текущей стоимости. Если оговоренная основная сумма свопа составляет $100, то текущая стоимость первого платежа по плавающей ставке и кривая доходности для 6-месячной ставки LIBOR рассчитывается по формуле 1.

Получив текущую стоимость потока наличности, можно рассчитать фиксированную ставку по формулы 1. Если С – фиксированная ставка, то:

Это означает, что фиксированная ставка в 9,28% даёт такой же доход, как и плавающая ставка в 9,00% и 9,57% по двум 6-месячным периодам.
Рассчитанное значение есть расчётная своп-ставка. Банк предлагает более низкую своп-ставку, чтобы обеспечить себе прибыль.
При таком подходе к оценке свопа результаты зависят от ставки, по которой дисконтируются потоки наличности. В примере 2 для определения доходности нулевого купона применялась спот-ставка, однако для периода между первой и второй купонной датой может быть использована и форвардная ставка.






